Committee
The committee is a group of 51 validators responsible for generating new blocks. Validators in the committee participate in the consensus algorithm by casting votes, with their voting power determined by their stake. While in the committee, validators cannot send Bond or Unbond transactions, meaning their voting power remains the same. The members of the committee changes randomly over time through Sortition transactions. Each block can contain zero or more Sortition transactions.
These rules are applied when committing sortition transactions:
- A minimum of ⅔ of the total stake must be maintained in the committee.
- If a validator is already in the committee, they will remain in the committee.
- If a validator is not in the committee, the oldest validator will exit the committee.
- Each validator should stay in committee at least for 51 blocks.
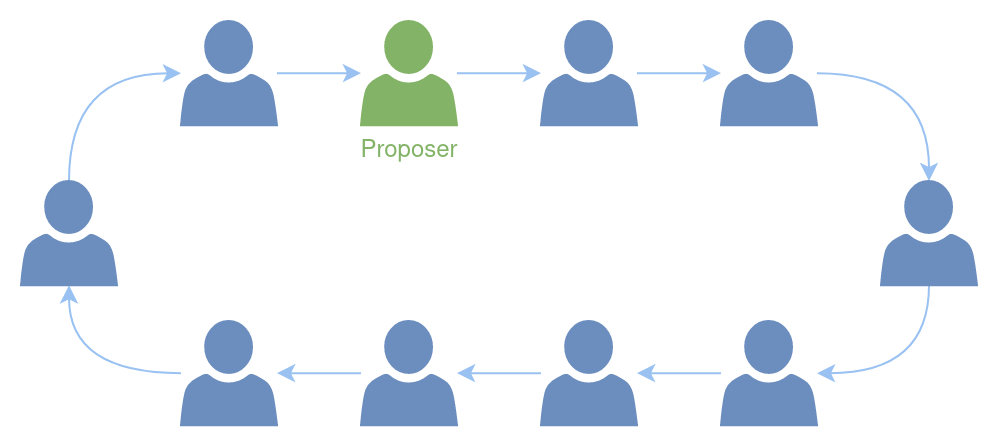
Proposer Selection
Proposer selection within the committee operates on a deterministic, clockwise rotation system. If a validator is unable to propose, for any reason, it stays within the committee, but the proposer’s role shifts to the next validator in the committee.
Adding Validators to the Committee
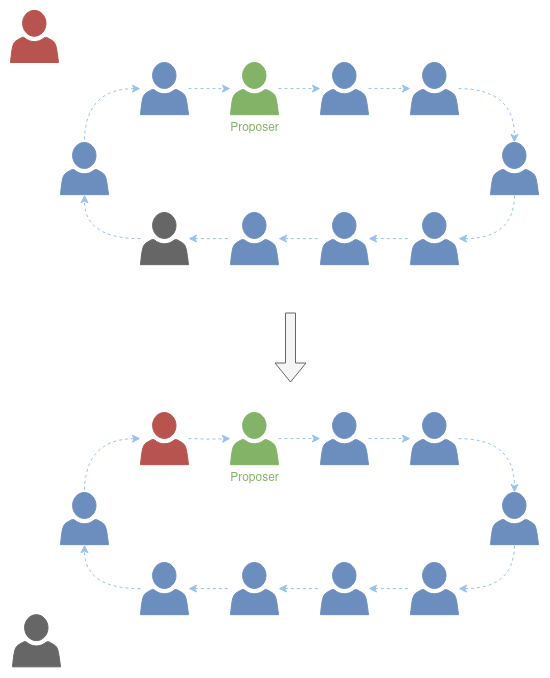
When a new validator joins the committee, they take a position before the current proposer. After the addition of a new validator, the committee adjusts to maintain the total number of validators at 51. This is achieved by removing the oldest validator from the committee, i.e., the one that has been in the committee for the longest time.
Security of the Committee
For an adversary to take control of the committee, they would need to control more than ⅔ of the stake within the committee. To assess the security of the committee, let’s assume all validators in the committee have the same voting power. In this case, an adversary would need to control more than ⅔ of the validators in the committee.
Now, let’s imagine an adversary holds 10% of the total stake. As a result, one of their validators can enter the committee every 10 blocks. In the first 10 blocks, one of the adversary’s validators enters the committee. In the next 10 blocks, another validator enters the committee, giving the adversary two validators within the committee. In the subsequent 10 blocks, another validator enters, but at the same time, the first validator leaves the committee. Therefore, an adversary with 10 10% of the total stake can have, on average, two validators in a committee of 51 validators.
Using the Poisson distribution, we can estimate the probability of an adversary controlling ⅔ of the committee:
| Adversarial Stake | Committee size | ⅔+ of committee | Adversarial committee members | Probability of controlling ⅔+ |
|---|---|---|---|---|
| 15% | 21 | 15 | 3 | \(5.46 \times 10^{-07}\) |
| 15% | 51 | 35 | 7 | \(3.34 \times 10^{-14}\) |
| 15% | 99 | 67 | 14 | \(1.41 \times 10^{-24}\) |
| 10% | 21 | 15 | 2 | \(3.39 \times 10^{-09}\) |
| 10% | 51 | 35 | 5 | \(1.90 \times 10^{-18}\) |
| 10% | 99 | 67 | 9 | \(2.91 \times 10^{-35}\) |
| 5% | 21 | 15 | 1 | \(2.81 \times 10^{-13}\) |
| 5% | 51 | 35 | 2 | \(4.50 \times 10^{-31}\) |
| 5% | 99 | 67 | 4 | \(1.09 \times 10^{-56}\) |
FAQ
How can one know when a validator has joined the committee?
The height at which the validator joined the committee is recorded as the “Last Joined Height” field in the validator structure. Once a validator enters the committee, this field is set to the current height it evaluated the sortition proof.
Can a validator within the committee run the sortition algorithm?
A validator within the committee can run the sortition algorithm. If they generate a valid sortition transaction, the height of their entry into the committee is set to the current block height, allowing them to stay in the committee for a longer period.